
von Guian Bolisay from NYC, USA (Slide Rule) [CC BY-SA 2.0 (http://creativecommons.org/licenses/by-sa/2.0)], via Wikimedia Commons
Der Rechenschieber sah wie ein Lineal aus, in dessen Mitte ein beweglicher Teil eingebaut war. Der Stab war ein analoges Rechenhilfsmittel (auch Analogrechner genannt, im Gegensatz zum digitalen Taschenrechner). Er zur mechanisch-grafischen Durchführung von Grundrechenarten, vorzugsweise der Multiplikation und Division, genutzt.
von Tangopaso (Eigenes Werk) [GFDL (http://www.gnu.org/copyleft/fdl.html) oder CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons
Ein Rechenschieber bestand aus mehreren beweglichen Teilen
Wollte man zum Beispiel die Rechnung 5X2 ausführen, musste die Ziffer „5“ auf dem beweglichen Teil über die „1“ auf dem festen Teil geschoben werden. Der Nutzer konnte dann über der Zahl „2“ auf dem festen Teil das Ergebnis ablesen – also in diesem Fall den Wert „10“.
„Das Prinzip eines Rechenschiebers besteht in der grafischen Addition oder Subtraktion von Strecken, die sich als logarithmische Skalen auf dem festen und dem beweglichen Teil des Rechenschiebers befinden. Bis zur weiten Verbreitung des Taschenrechners, die in den 1970er Jahren begann, waren Rechenschieber für viele Berechnungen in Schule, Wissenschaft und Technik unentbehrlich“, berichtet das Internetportal Wikipedia.de“.
Mehr Infos: https://de.wikipedia.org/wiki/Rechenschieber
Heiner Brünjes


Das ist ein guter Anfang.
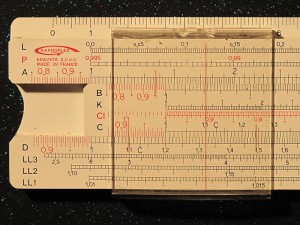
Ich erkläre hier mal, was ich vorne auf dem Rechenschieber, der bei Ihnen rechts auf dem Bild zu sehen ist, erkenne und schreibe es auf. Sie sehen die Buchstaben L,P,A,B, K, Cl, C, D,LL3, LL2,LL1. Jeder hat seine eigene Bedeutung und Anordnung.
C und D sind die „Grundskalen“, die direkt miteinander Ergebnisse wie die der Multiplikation und der Division zeigen.
L ist die Mantissenskala (lg x),
P ist die pythagoreische Skala, Funktion y=Wurzel 1-x² => zB für zB. Hochfrequenztechnik/Elektrobereich auch
Handyfunktechnik
A ist die Quadratskala , Funktion x² , auf der unbeweglichen „Körperleiste“
B ist die Quadratskala, so., aber auf der „Zunge“ des Rechenstabes/Rechenschiebers, ab jetzt RS abgekürzt
K ist die Kubikskala, x³ auf der oberen Körperleiste des RS
Cl ist die Kehrwertskala zu C Funktion 1/x auf der beweglichen „Zunge“ des RS
C ist die Grundskala Funktion X
D ist die Grundskala Funktion X , zusammen mit C die „Grundrechenarten“ Multiplikation,Division
LL1 ist die Expotentialskala Bereich: 0,1-1,10 e^0,01x
LL2 ist die Expotentialskala Bereich 2:1,1-3, e^0,1x
LL3 ist die Expotentialskala Bereich 2,5 – 50.000 e^x
Auf der Rückseite der Zunge ist oft noch eine Erweiterung der Skalen, so dass neue Funktionen dazukommen, wenn die Zunge umgedreht wird. Aber schon dieser einseitige RS ermöglicht sehr, sehr viele Rechnvorgänge, so dass man sehr einfach durch Verschieben der Zunge und des Läufers schwierige Rechenoperationen blitzschnell ablesen konnte.
Es gibt natürlich Rechnungen mit Zwischenschritten. Eine ganze Menge der Rechenschritte sind von einem geübeten RS-Benutzer übrigens tatsächlich schneller zu berechnen bzw die Ergebnisse zu präsentieren, als wenn jemand einen Taschenrechner benutzte. Schließlich müssen die vielen Zahlen nicht erst eingegeben werden.
Als die Astronauten das erste Mal auf dem Mond landeten, hatten sie trotz des bereits sich manifestierten elektronischen Taschenrechners einen Rechenschieber mit sich, denn sie wussten nicht, ob ein Taschenrechner mit Batterien dort funktionierte, beim Rechenschieber/Rechenstab war es logisch, dass er funktionieren würde, und er tat es sehr gut.
Zuerst wurden Rechenschieber aus Mahagoni oder Buche hergestellt, mit stabilisierenden Stahlbändern im Holz je Leiste, durch federnde Stahllamellen miteinander verbunden, die zur evtl notwendig werdenden Justierung bei Witterungseinflüssen ab und zu aufgeschraubt werden konnten.Später wurde weißes Celluloid auf die Skalenleisten aufgetragen, das sich schnell großer Beliebtheit erfreute. Sowohl Faber Castell mit dem eigens für die RS erforschten und GEROPLAST genannten Kunststoff als auch ARISTO mit ihrem ARISTOPAL genannten Kunststoffstellten schließlich Rechenstäbe ganz aus ihrem Material her, wärmeunempfindlich bis 70°C, bruchsicher sehr flexibel (gegen Holz) und unempfindlich gegen Tusche etc, wenn man sie schnell wegwischte …und andere gute Eigenschaften mehr, hatten schließlich einen idealen Kunststeff entwickelt, so dass die hölzernen – und wesentlich dickeren – RS nicht mehr benötigt wurden. Eine Zeitlang konnte gewählt werden, ob man den RS aus Holz [mit Celluloid] oder aus Geroblast bzw Aristopal kaufen wollte, aber dies währte nur kurz. Die Rechenstäbe/Schieber waren erst in Deutschland, dann in den USA mit Extraanpassungen, dann in China und schnell weltweit in Gebrauch. Selbst heute kommt man bis zum Ende der 10 Klasse Gymansium mit dem richtigen Rechenschieber :urecht, wenn man will.
Aber auf dem Taschnrechner Knöpfe drücken ist einfacher ales eine Rechenopation mit dem Kopf zu begleiten und nach 3 Nachkommastellen den Rest im Kopf auszurechnen, daher wurde der Taschenrechner DAS Instrument der Mathematik.
Es gab Übrgens Rechenschieber/stäbe für Volksschulen,Mittelschulen, 4öhere „Lehranstalten“, sowie Berufs-und Berufsfachschulen, Handelsschulen etc, Kaufleute, Techn. Kaufleute, Bautechniker und Maschinenbauer, Maschinenbauer und Elektrotechniker, Studierende an Techn.Hoch-und Ing.-Schulen, Ingenieure aller Fachrichtungen.
Da sieht man, wie hochspezialisiert Rechnschieber waren, wie genau welche Skalen für welche Rechenschieber benötigt wurden und entsprechend zusammengesetzt wurden. Das sind schon wahre Schätze und wer einen Rechenschieber z.H. hat, kann ihn – wieder – erlernen. Es macht oft Spaß, mir sogar sehr, was ich früher nie für möglich gehalten hätte, ich war abgestempelt als die, die in Mathe so gerad noch am Ende eine Vier hatte, zwischendurch auch mal eine Fünf auf dem Zeugnis. Heute gebe ich Nachhilfe, z.Zt einem 9.-Klässler, Gymnasium. Man tut auf jeden Fall was für sein Hirn und gegen Langeweile. Ich persönlich wollte zunächst nur was für mein Hirn tun, dann jedoch verstand ich die Mathematik immer mehr, es wurde interessanter und ich fand so Zugang zu ihr, die ich jahrzehntelang als „Feind“ in Erinnerung hatte, der mir abverlangte, wofür ich als „zu dumm“ bezeichnet wurde, trotz guten Abiturs. Heute nutze ich ihn, um meinem Nachhilfeschüler Mathe zu erklären, wo meine Worte nicht reichen. Mathe ist hier begreifbar. Zahlenstrahle kennen wir alle und beim Rechenstab/-schieber rechnet man mit Skalen, das sind Zahlenstrahle. Richtig klasse, das Teil! Es sollte in der Schule einen Block lang unterrichtet werden. Dann würden wohl viele Kinder mehr auch einen besseren Zugang zur Mathematik finden.
Es gibt einige Rechtschreibfehler, die ich nicht verhindern konnte. Durch mehrere Behinderungen, u. a. ständiges Zittern, ist es mir auch nach mehreren Versuchen zuweilen nicht möglich, die richtige Taste zu drücken und beim Nachsehen weiß mein Hirn ja, was da stehen SOLLTE und überliest teils die Fehler. Ich bitte um Entschuldigung. Nach meinem Dafürhalten kann jeder verstehen, was ich ausdrücken will. Besser kann ich es nicht mehr. Früher schon, doch ich muss damit leben, was ich heute noch kann und bitte Sie, mich so zu akzeptieren, wie ich heute bin.
„Nicht perfekt ist auch gut.“
Diesen Satz auf einer Karte schenkte mir neulich jemand. Das trifft auf mich auch zu. Der Satz und was dahinter steckt, tut mir sehr nachhaltig gut.
Danke!